Skip to contents

LMMsolver

CRAN RStudio mirror downloads R-CMD-check codecov

The aim of the LMMsolver package is to provide an efficient and flexible system to estimate variance components using restricted maximum likelihood or REML (Patterson and Thompson 1971), for models where the mixed model equations are sparse. An important feature of the package is smoothing with P-splines (Eilers and Marx 1996). The sparse mixed model P-splines formulation (Boer 2023) is used, which makes the computations fast.

Installation

  • Install from CRAN:
install.packages("LMMsolver")
  • Install latest development version from GitHub (requires remotes package):
remotes::install_github("Biometris/LMMsolver", ref = "develop", dependencies = TRUE)

Example

As an example of the functionality of the package we use the USprecip data set in the spam package (Furrer and Sain 2010).

library(LMMsolver)
library(ggplot2)

## Get precipitation data from spam
data(USprecip, package = "spam")

## Only use observed data.
USprecip <- as.data.frame(USprecip)
USprecip <- USprecip[USprecip$infill == 1, ]
head(USprecip[, c(1, 2, 4)], 3)
#>      lon   lat  anomaly
#> 6 -85.95 32.95 -0.84035
#> 7 -85.87 32.98 -0.65922
#> 9 -88.28 33.23 -0.28018

A two-dimensional P-spline can be defined with the spl2D() function, with longitude and latitude as covariates, and anomaly (standardized monthly total precipitation) as response variable:

obj1 <- LMMsolve(fixed = anomaly ~ 1,
                 spline = ~spl2D(x1 = lon, x2 = lat, nseg = c(41, 41)),
                 data = USprecip)

The spatial trend for the precipitation can now be plotted on the map of the USA, using the predict function of LMMsolver:

lon_range <- range(USprecip$lon)
lat_range <- range(USprecip$lat)
newdat <- expand.grid(lon = seq(lon_range[1], lon_range[2], length = 200),
                      lat = seq(lat_range[1], lat_range[2], length = 300))
plotDat <- predict(obj1, newdata = newdat)

plotDat <- sf::st_as_sf(plotDat, coords = c("lon", "lat"))
usa <- sf::st_as_sf(maps::map("usa", regions = "main", plot = FALSE))
sf::st_crs(usa) <- sf::st_crs(plotDat)
intersection <- sf::st_intersects(plotDat, usa)
plotDat <- plotDat[!is.na(as.numeric(intersection)), ]

ggplot(usa) + 
  geom_sf(color = NA) +
  geom_tile(data = plotDat, 
            mapping = aes(geometry = geometry, fill = ypred), 
            linewidth = 0,
            stat = "sf_coordinates") +
  scale_fill_gradientn(colors = topo.colors(100))+
  labs(title = "Precipitation (anomaly)", 
       x = "Longitude", y = "Latitude") +
  coord_sf() +
  theme(panel.grid = element_blank())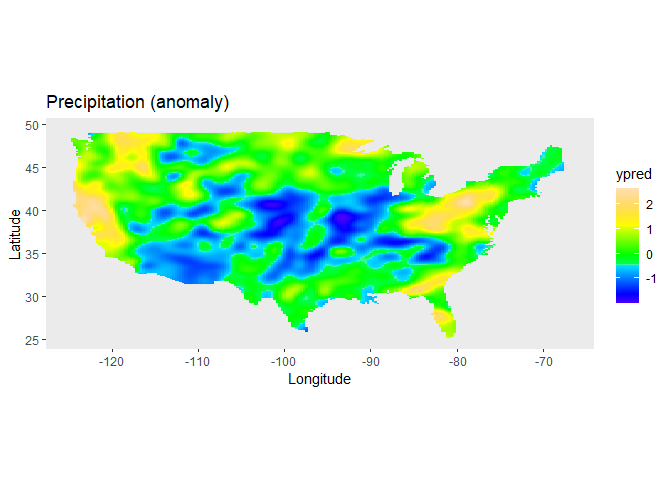

Precipitation anomaly USA

Further examples can be found in the vignette.

vignette("Solving_Linear_Mixed_Models")

References

Boer, Martin P. 2023. “Tensor Product P-Splines Using a Sparse Mixed Model Formulation.” Statistical Modelling 23 (5-6): 465–79. https://doi.org/10.1177/1471082X231178591.
Eilers, PHC, and BD Marx. 1996. “Flexible smoothing with B-splines and penalties.” Stat. Sci. https://www.jstor.org/stable/2246049.
Furrer, R, and SR Sain. 2010. “spam: A sparse matrix R package with emphasis on MCMC methods for Gaussian Markov random fields.” J. Stat. Softw. https://core.ac.uk/download/pdf/6340272.pdf.
Patterson, HD, and R Thompson. 1971. “Recovery of inter-block information when block sizes are unequal.” Biometrika. https://doi.org/10.1093/biomet/58.3.545.