Skip to contents

statgenHTP tutorial: 3. Correction for spatial trends

Emilie Millet, Bart-Jan van Rossum, Diana Marcela Perez Valencia, Maria Xose Rodriguez Alvarez, Fred van Eeuwijk

2022-12-13

Source: vignettes/vignettesSite/SpatialModel_HTP.Rmd
SpatialModel_HTP.Rmd

Introduction

Phenotyping facilities display spatial heterogeneity. For example, the spatial variability of incident light can go up to 100% between pots within a greenhouse (Cabrera-Bosquet et al. 2016). Taking into account these spatial trends is a prerequisite for precise estimation of genetic and treatment effects. In the same way as in field trials, platform experiments should obey standard principles for experimental design and statistical modeling.

Popular mixed models to separate spatial trends from treatment and genetic effects, rely on the use of autoregressive correlation functions defined on rows and columns (AR1×AR1) to model the local trends (Cullis, Smith, and Coombes 2006). These models are sometimes difficult to fit and the selection of a best model is complicated, therefore preventing an automated phenotypic analysis of series of trials. An attractive alternative is the use of 2-dimensional P-spline surfaces, the SpATS model (Spatial Analysis of Trials using Splines, (Rodríguez-Álvarez et al. 2018)). This model corrects for spatial trends, row and column effects and has the advantage of avoiding the model selection step. It also provides the user with graphical outputs that are easy to interpret. It has proven to be a good alternative to the classical AR1×AR1 modeling in the field (Velazco et al. 2017). It is also suitable for phenotyping platform data and has been tested on several datasets in the EPPN2020 project.

The aim of this document is to accurately separate the genetic effects from the spatial effects at each time point. It will provide the user with either genotypic values or corrected values that can be used for further modeling. In brief, separately for each measurement time \(t\), a spatial model is fitted for the trait \(y_t\),

\(y_t = 1_M \beta_{0t} + X_h \beta_{ht} + X_q \beta_{qt} + Z_g c_{gt} + f_t(u,v) + Z_r c_{rt} + Z_c c_{ct} + \epsilon_t\)

where briefly,

  • \(1_M \beta_{0t}\), is the intercept,
  • \(X_h \beta_{ht}\), corresponds to the factors/covariates whose effects we are interested in modeling,
  • \(X_q \beta_{qt}\), corresponds to the factors/covariates whose effects we are interested in removing,
  • \(Z_g c_{gt}\), corresponds the genotypic effects,
  • \(f_t(u,v) + Z_r c_{rt} + Z_c c_{ct}\), represents the spatial effects, with \(f_t(u,v)\) corresponding to the spatial function, e.g. the PSANOVA function from the SpATS package, \(Z_r c_{rt}\) and \(Z_c c_{ct}\) represent the design matrices and effects for the random row and column effects respectively,
  • \(\epsilon_t\), is the residual.

For more details see Pérez-Valencia et al. (2022).

This tutorial describes in detail how to perform analyses to correct for spatial trends using different modeling engines and how to extract the results from the models.

Modeling with spatial terms using Example 1

We will use the TP object phenoTPOut in which annotated time points were replaced by NA because they were considered to be outliers. (see statgenHTP tutorial: 2. Outlier detection for single observations).

After creating a TP object, a model can be fitted on the data. This is done using the function fitModels, which uses two different engines for fitting the models, namely SpATS (Rodríguez-Álvarez et al. 2018) and ASReml (Butler et al. 2017). For models with row and column coordinates, SpATS is the default engine (see section 2.1). This can be overruled by specifying the function parameter engine and using ASReml for spatial models (see section 2.2). When the row and column coordinates are not available, ASReml is used for modeling without spatial components (see section 3). Finally, it is possible to decompose the genotypic variance using, for example, a treatment effect (see section 4).

The output of fitModels is an object of class fitMod, a list of fitted models with one item for each time point the model was fitted for.

Spatial model using SpATS

When SpATS is used for modeling, an extra spatial term is included in the model. This spatial component is composed using the PSANOVA function in the SpATS package which uses 2-dimensional smoothing with P-splines as described in Lee, Durbán, and Eilers (2013) and in Rodríguez-Álvarez et al. (2018). See help(PSANOVA, SpATS) for a detailed description. Extra fixed effects may be fitted using the option extraFixedFactors. The model can also be fitted following a resolvable row-column design setting useRepId as TRUE.

The model specifications are listed in the table below with a simplified model.

OPTION MODEL FITTED SPATIAL TERM
default \(y\) = \(\mu\) + genotype + rowId + colId + \(\epsilon\) PSANOVA
extraFixedFactors = c(“A”, “B”) \(y\) = \(\mu\) + A + B + genotype + rowId + colId + \(\epsilon\) PSANOVA
useRepId = TRUE \(y\) = \(\mu\) + repId + genotype + repId:rowId + repId:colId + \(\epsilon\) PSANOVA
useCheck = TRUE \(y\) = \(\mu\) + check + genoCheck + rowId + colId + \(\epsilon\) PSANOVA

In the models above, fixed effects are indicated in italics whereas random effects are indicated in bold. “genotype” can be fitted as random or fixed effect using the option what. The option useCheck allows treating some genotypes as check: it splits the column “genotype” into two columns as follows:

genotype check genoCheck
G1 noCheck G1
G2 noCheck G2
… noCheck …
Gn-1 noCheck Gn-1
Gn noCheck Gn
check1 check1 NA
check2 check2 NA
… … …
checkm-1 checkm-1 NA
checkm checkm NA

NOTE: It is only possible to use the combination of check and genotype as random.

Calling SpATS

Using the TP object phenoTPOut from the previous vignette, a model for a few time points and trait “EffpsII” can now be fitted on the data as follows. Since engine is not supplied as an option, SpATS is used for fitting the following model:
EffpsII = \(\mu\) + genotype + rowId + colId + \(\epsilon\)

## Fit a model for a few time points.
modPhenoSp <- fitModels(TP = phenoTPOut, 
                        trait = "EffpsII",
                        timePoints = seq(from = 1, to = 73, by = 5)) 
summary(modPhenoSp)
#> Models in modPhenoSp where fitted for experiment Phenovator.
#> 
#> It contains 15 time points.
#> The models were fitted using SpATS.

The output is a fitMod object, a list containing one fitted model per time point. Note that by not supplying the what argument to the function, genotype is set as random. It can be run again with genotype as fixed using what:

EffpsII = \(\mu\) + genotype + rowId + colId + \(\epsilon\)

## Fit a model for a single time point.
modPhenoSpFix <- fitModels(TP = phenoTPOut, 
                           trait = "EffpsII",
                           timePoints = 3,
                           what = "fixed")

The model can be extended by including extra main fixed effects, here to include extra experimental design factors:
EffpsII = \(\mu\) + repId + Image_pos + genotype + rowId + colId + \(\epsilon\)

## Fit a model for a single time point with extra fixed factors.
modPhenoSpCov <- fitModels(TP = phenoTPOut, 
                           trait = "EffpsII",
                           extraFixedFactors = c("repId", "Image_pos"), 
                           timePoints = 3)

It can be further extended by including check genotypes:
EffpsII = \(\mu\) + repId + Image_pos + check + genoCheck + rowId + colId + \(\epsilon\)

## Fit a model for a single time point with extra fixed effects and check genotypes.
modPhenoSpCheck <- fitModels(TP = phenoTPOut, 
                             trait = "EffpsII",
                             extraFixedFactors = c("repId", "Image_pos"),
                             useCheck = TRUE,
                             timePoints = 3)

Finally, a model following a resolvable row-column design can be fitted: including the effects of row and column nested within replicate.
EffpsII = \(\mu\) + repId + genotype + repId:rowId + repId:colId + \(\epsilon\)

## Fit a model for a single time point.
modPhenoSpRCD <- fitModels(TP = phenoTPOut,
                           trait = "EffpsII",
                           timePoints = 3,
                           useRepId = TRUE)

Model plots

The first type of plot that can be made for fitted models, is a spatial plot per time point using plotType = "spatial". It consists of plots, spatial plots of the raw data, fitted values, residuals and either BLUEs or BLUPs, and a histogram of the BLUEs or BLUPs. When SpATS is used for modeling an extra plot with the fitted spatial trend is included (see (Rodríguez-Álvarez et al. 2018) and (Velazco et al. 2017) for interpretation).

Note that spatial plots can only be made if spatial information, i.e. rowNum and colNum, is available in the TP object.

plot(modPhenoSp,
     timePoints = 36,
     plotType = "spatial",
     spaTrend = "raw")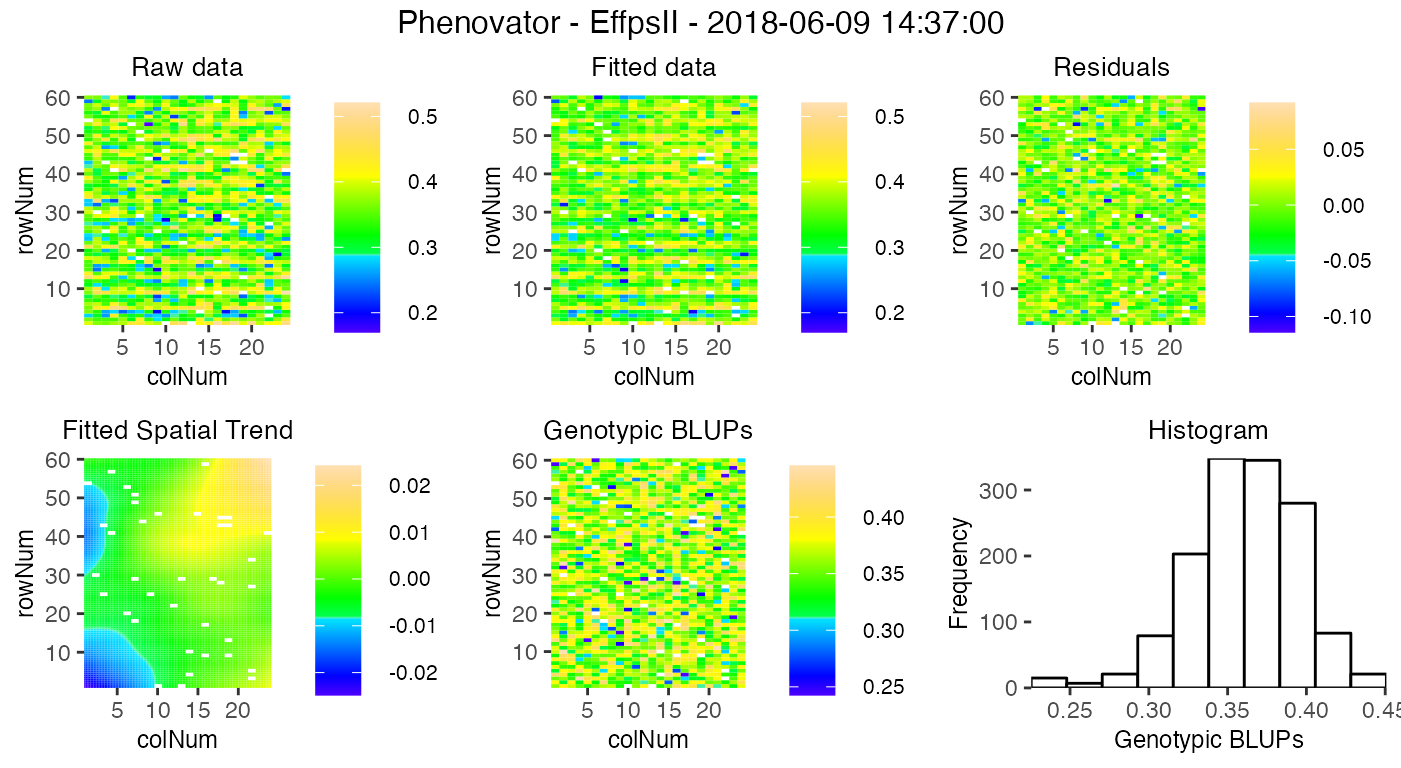

For assessing the importance of the fitted spatial trends at one glance, and for comparison between time points, the plot of the fitted spatial trend can be displayed as a ratio of the raw phenotypic mean: SpatTrend(proportion) = Estimated SpatTrend / mean(raw EffpsII). In this case, the scale will be in percentage and the min/max will be adjusted based on all the time points used but will be at least 10%. This empirical threshold allows visualizing fitted trends that have a relatively small to large importance.

plot(modPhenoSp,
     timePoints = 36,
     plotType = "spatial",
     spaTrend = "percentage")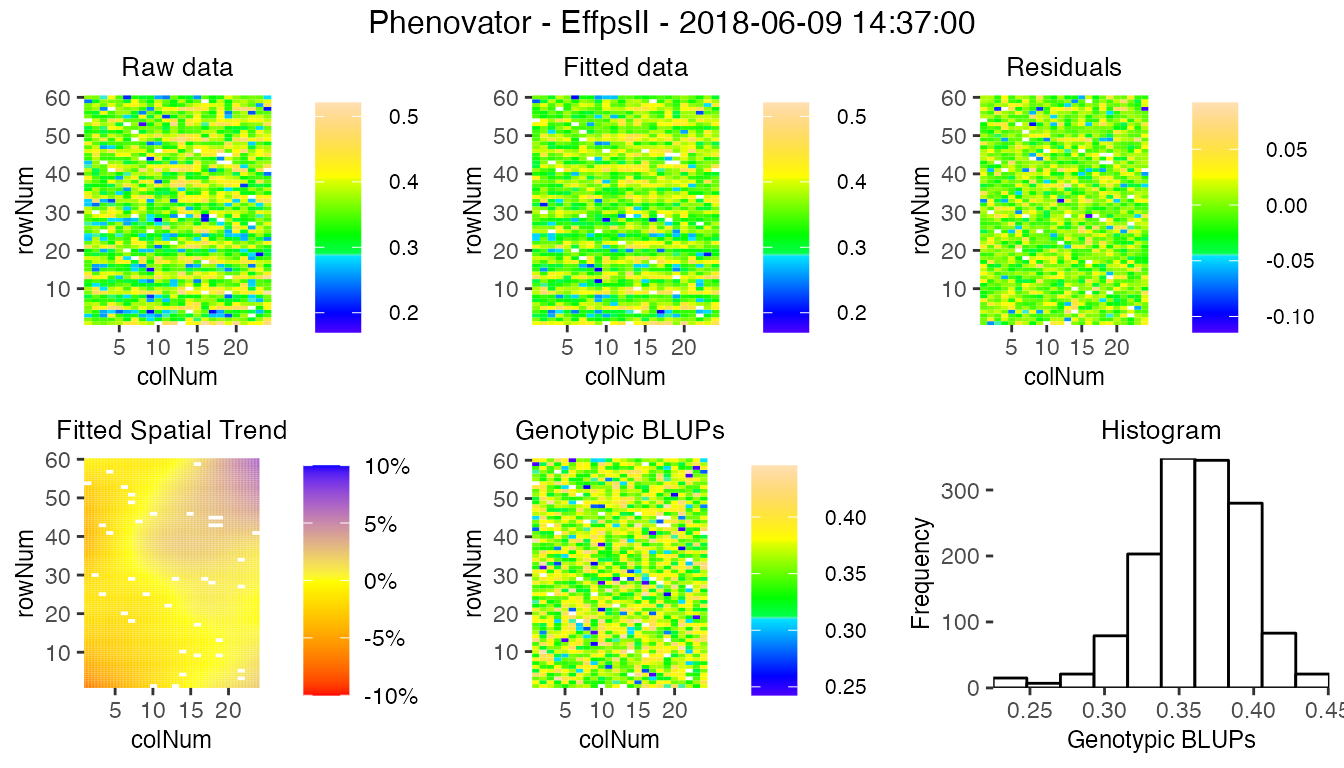

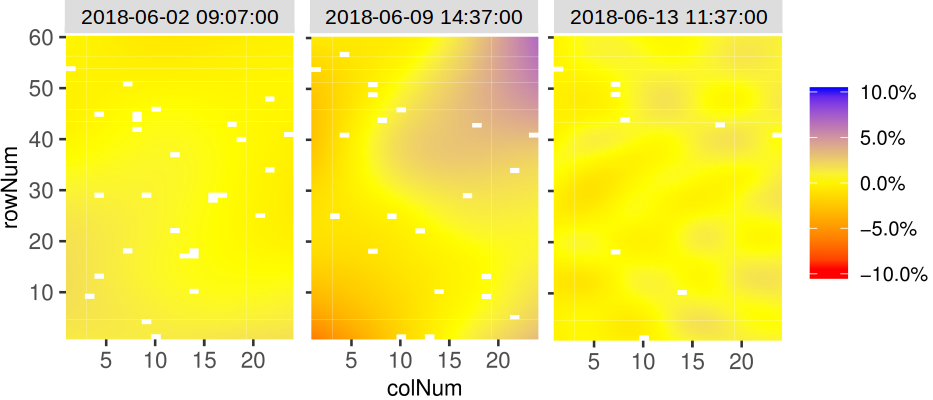
It is also possible to create a time lapse of the ratio of spatial trends over time. The scale is the same as previously described. The time lapse is always written to an output file.

plot(modPhenoSp, 
     plotType = "timeLapse",
     outFile = "TimeLapse_modPhenoSp.gif")

Here is an illustration with three time points:

Extracting model results

All results that can be extracted are shown in the table below. The first column contains the function names. The second column contains a short description of the result that will be extracted and, where needed, states for which modeling engines it can be extracted.

FUNCTION DESCRIPTION
getGenoPred Best Linear Unbiased Predictions (BLUPS, genotype as random) or Estimators (BLUEs, genotype as fixed)
getCorrected Spatially corrected values at the experimental unit level
getVar Variance components
getHerit Generalized heritabilities - only when genotype is random
getEffDims Effective dimensions - only for SpATS engine

By default, all the functions run for all the time points. It is possible to select some of them using timePoints. The ratio of the effective dimensions can also be extracted using EDType = "ratio" in the getEffDims function.

The output of the function getGenoPred is a list of two dataframes: “genoPred” which contains the predicted values for all tested genotypes and “checkPred” which contains the predicted values of the check genotypes, when useCheck = TRUE in the model. “checkPred” is empty when useCheck = FALSE.

## Extract the genotypic predictions for one time point: 
genoPredSp <- getGenoPred(modPhenoSp, timePoints = 6)
## Extract the corrected values for one time point: 
spatCorrSp <- getCorrected(modPhenoSp, timePoints = 6)
## Extract model components: 
varianceSp <- getVar(modPhenoSp)
heritSp    <- getHerit(modPhenoSp)
effDimSp   <- getEffDims(modPhenoSp)

The genotypic predictions of the test genotypes for one time point are displayed in a table like the following:

timeNumber timePoint genotype predicted.values standard.errors
6 2018-06-02 09:07:00 check1 0.6659103 0.0042991
6 2018-06-02 09:07:00 check2 0.5894471 0.0059116
6 2018-06-02 09:07:00 check3 0.6675676 0.0057804
6 2018-06-02 09:07:00 check4 0.6746556 0.0042381
6 2018-06-02 09:07:00 G001 0.6664412 0.0077009
6 2018-06-02 09:07:00 G002 0.6650949 0.0077011

The corrected values are obtained by considering only the estimated sources of variation which are of interest. Here, the correction follows the procedure described in (Welham et al. 2004). They propose a partition of the explanatory variables in three groups: (i) those for which predicted values are required (i.e. population and genotypic effects), (ii) those to be averaged over (i.e. experimental factors effects), and (iii) those to be ignored (i.e. spatial effects). The corrected trait is obtained as follows (in simplified terms, for full explanation see Pérez et al. (in prep)): \(\tilde{y}_t = \hat \mu_t + \widehat{geno}_t + \widehat{fixed}_t + \hat{\epsilon}_t\)
where \(\widehat{fixed}_t\) are the fixed covariates of interest (e.g. population effect).

This allows keeping the data at the experimental unit level (plants) and having more degrees of freedom for further modeling (e.g. time course modeling and estimation of the time course parameter(s)).

NOTE: The estimated fixed effects included in extraFixedFactors are removed from the corrected phenotype (\(\tilde{y}_t\)).

The corrected values of one time point are displayed in a table like the following:

timeNumber timePoint EffpsII_corr EffpsII wt genotype rowId colId plotId
6 2018-06-02 09:07:00 0.6472045 0.645 1756.311 check1 28 11 c11r28
6 2018-06-02 09:07:00 0.6477295 0.658 1756.311 check1 10 16 c16r10
6 2018-06-02 09:07:00 0.6854932 0.678 1756.311 check1 56 9 c9r56
6 2018-06-02 09:07:00 0.6589555 0.669 1756.311 check1 30 4 c4r30
6 2018-06-02 09:07:00 0.6698425 0.669 1756.311 check1 4 20 c20r4
6 2018-06-02 09:07:00 0.6804443 0.679 1756.311 check1 35 13 c13r35

Plotting model results

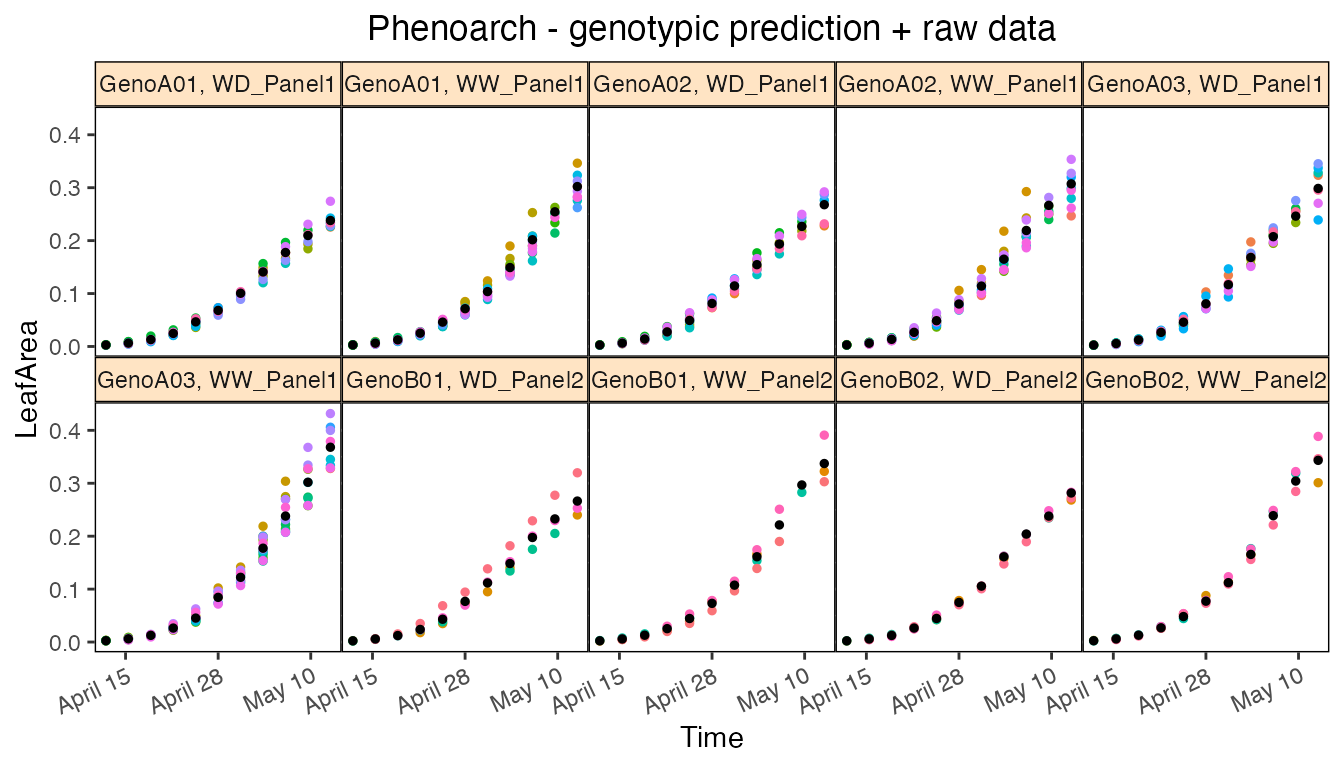
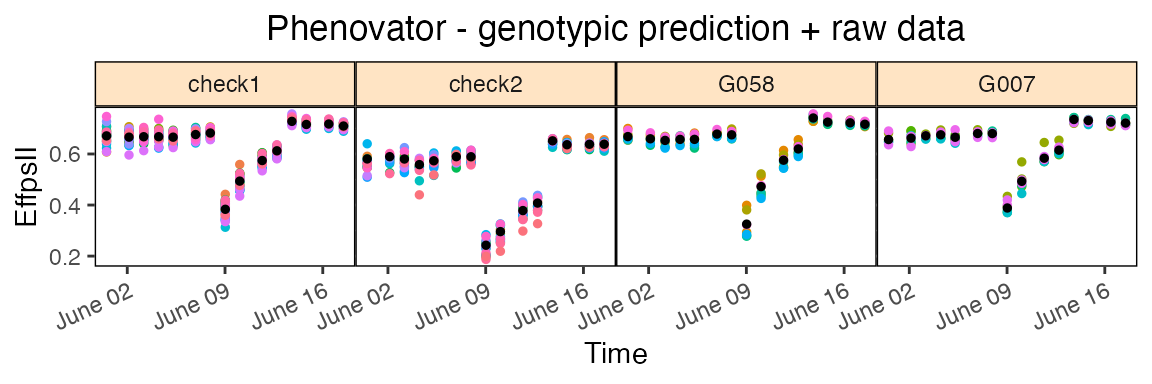
Different plots can be displayed for the fitMod object. The first one is rawPred, it plots the raw data (colored dots, one color per plotId) overlaid with the predicted values (black dots) from the fitted model. One plot is made per genotype with all its plotId. These plots are put together in a 5×5 grid per page.
Using the parameter genotypes, a subset of genotypes will be plotted. By default, data are plotted as dots but this can be changed by setting plotLine = TRUE.

plot(modPhenoSp, 
     plotType = "rawPred",
     genotypes = c("check1", "check2", "G007", "G058"))

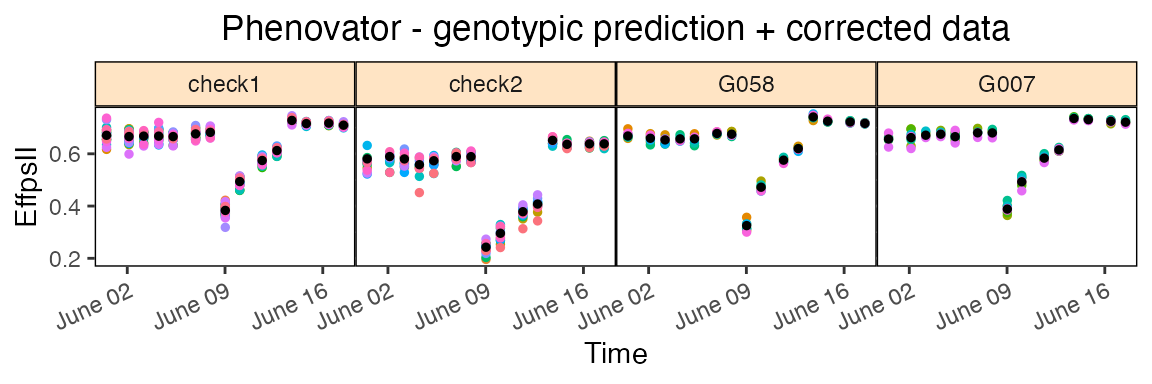
The second one is corrPred, it plots the spatially corrected data (colored dots, one color per plotId) overlaid with the predicted values from the fitted model (black dots). One plot is made per genotype with all its plotId. These plots are put together in a 5×5 grid per page.
Using the parameter genotypes, a subset of genotypes will be plotted. By default, data are plotted as dots but this can be changed by setting plotLine = TRUE.

plot(modPhenoSp, 
     plotType = "corrPred",
     genotypes = c("check1", "check2", "G007", "G058") )

Note that when check genotypes are used for modeling, for the two previous plot types (rawPred and corrPred), the parameter plotChecks should be set to TRUE to display check genotypes.

plot(modPhenoSpCheck, 
     plotType = "rawPred",
     plotChecks = TRUE,
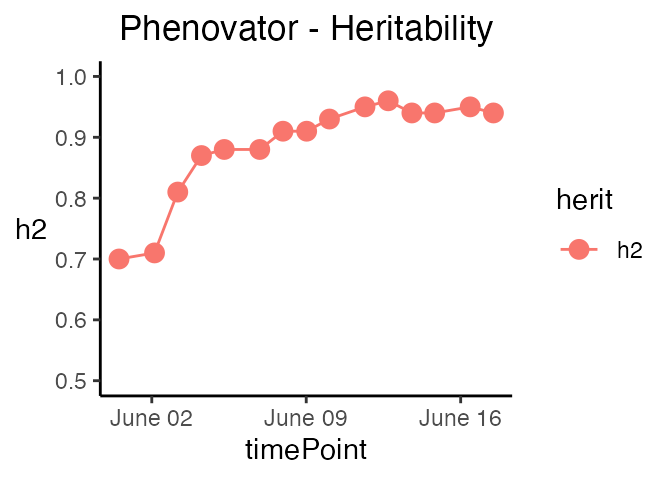
     genotypes = c("check1", "check2", "G007", "G058"))

The last three types of plot display different model parameters over time. Plot type herit plots the heritability over time. If geno.decomp is used when fitting the model, heritabilities are plotted for each level of the genotype groups in a single plot (see section 4). The scale of the plot can be adjusted using yLim.

plot(modPhenoSp, 
     plotType = "herit",
     yLim = c(0.5, 1))

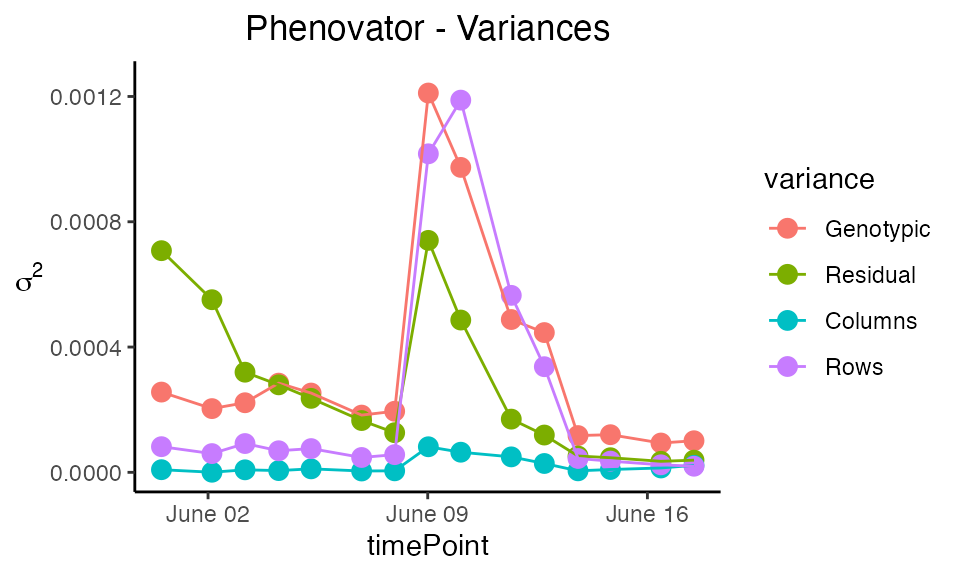
Plot type variance plots the residual, column and row variances over time. These plots can serve as diagnostics of the experiment. The scale of the plot can be adjusted using yLim.

plot(modPhenoSp, 
     plotType = "variance",
     yLim = c(0, 0.00125))

Plot type effDim plots the effective dimension from models fitted using SpATS over time. By default, all the spatial components are plotted. This can be restricted using the option whichED. The scale of the plot can be adjusted using yLim.

plot(modPhenoSp, 
     plotType = "effDim",
     whichED = c("colId", "rowId", "fColRow","colfRow", "surface"),
     EDType = "ratio")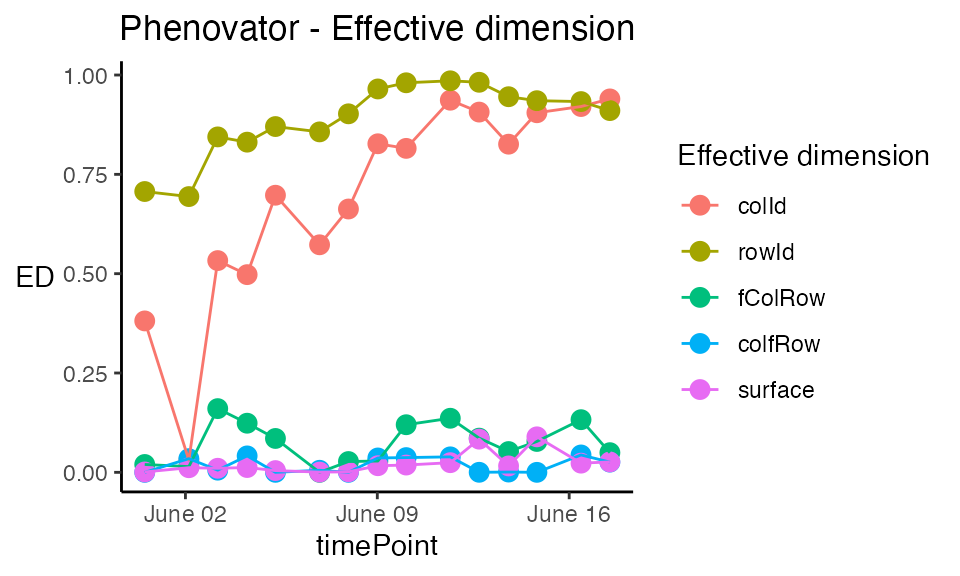

The effective dimensions are also known as the effective degrees of freedom. They can be interpreted as a measure of the complexity of the corresponding component: if the effective dimension of one component is large, it indicates that there are strong spatial trends in this direction. For better comparison between components, the ratio of effective dimensions vs. total dimensions can be used. It has a value between 0, no spatial trend, and 1, strong spatial trend (almost all the degrees of freedom are used to model it).

The table below gives an overview of the effective dimensions and an explanation of their meaning.

EFFECTIVE DIMENSION EXPLANATION
colId Linear trend along columns
rowId Linear trend along rows
fCol Smooth trend along columns
fRow Smooth trend along rows
fColRow Linear trend in rows changing smoothly along cols
colfRow Linear trend in cols changing smoothly along rows
fColfRow Smooth-by-smooth interaction trend over rows and cols
surface Sum of smooth trends

Spatial model with ASReml

When ASReml is used for modeling and spatial = TRUE, four models are fitted with different random terms and covariance structures. The best model is determined based on a goodness-of-fit criterion, AIC, on 20% of the time points or at least 10 time points. The best model is then run on all time points. As for SpATS, all the ASReml models can be extended by fitting extra fixed factors using the option extraFixedFactors.

Note that for the moment, it is only running with ASReml-R version 4 or higher.

OPTION MODEL FITTED SPATIAL TERM
spatial = TRUE \(y\) = \(\mu\) + genotype + row + col + \(\epsilon\) AR1(rowId):AR1(colId)
AR1(rowId):colId
rowId:AR1(colId)
-
spatial = TRUE, extraFixedFactors = c(“A”, “B”) \(y\) = \(\mu\) + A + B + genotype + row + col + \(\epsilon\) AR1(rowId):AR1(colId)
AR1(rowId):colId
rowId:AR1(colId)
-
spatial = TRUE, repID = TRUE \(y\) = \(\mu\) + repId + genotype + repId:row + repId:col + \(\epsilon\) AR1(rowId):AR1(colId)
AR1(rowId):colId
rowId:AR1(colId)
-

In the models above, fixed effects are indicated in italics whereas random effects are indicated in bold. “genotype” can be fitted as random or fixed effect using the option what. The option useCheck is not displayed in the table but works the same as for SpATS: treating some genotypes as check (see section 2.1 for details).

Calling ASReml is done by changing the engine option in the fitModels function.

if (requireNamespace("asreml", quietly = TRUE)) {
  ## Fit a model on few time points with spatial function:
  modPhenoSpAs <- fitModels(TP = phenoTPOut, 
                            trait = "EffpsII",
                            timePoints = seq(from = 1, to = 73, by = 5),
                            engine = "asreml",
                            spatial = TRUE) 
  summary(modPhenoSpAs)
}

Here the best spatial model is: trait = genotype + row + col + \(\epsilon\), with a spatial component: AR1(rowId):AR1(colId). It has been selected using 10 time points.

Plotting and extracting results is then done the same way as for SpATS. Below are a few examples.

if (requireNamespace("asreml", quietly = TRUE)) {
  spatCorrSpAs <- getCorrected(modPhenoSpAs, timePoints = 6)
}
if (requireNamespace("asreml", quietly = TRUE)) {
  plot(modPhenoSpAs, 
       plotType = "herit",
       yLim = c(0.5, 1))
}

Note that when the engine is ASReml, the heritability is calculated using the formula provided in (Cullis, Smith, and Coombes 2006).

Modeling without spatial terms with ASReml

When the row and column coordinates are not available, only ASReml can be used for modeling. In that case, the model simply uses the genotype and the extraFixedFactors, if any.

OPTION MODEL FITTED SPATIAL TERM
spatial = FALSE \(y_t\) = genotype + \(\epsilon\) -
spatial = FALSE, extraFixedFactors = c(“A”, “B”) \(y_t\) = A + B + genotype + \(\epsilon\) -

In the models above and below, fixed effects are indicated in italics whereas random effects are indicated in bold. genotype can be fitted as random or fixed effect using the option what. The option useCheck is not displayed in the table, but works the same as for SpATS (see section 3.1).

## Fit a model on few time points without spatial function.
modPhenoAs <- fitModels(TP = phenoTPOut, 
                        trait = "EffpsII",
                        timePoints = seq(from = 1, to = 73, by = 5),
                        engine = "asreml",
                        spatial = FALSE)

Modeling with decomposition of genotypes using Example 2

When an experimental treatment is applied, for example, a water scenario, it is required to decompose the genotypic variance into the levels of the treatment. In the following example, two water scenarios, well-watered (WW) and water deficit (WD), were applied. Thus, instead of modeling one genotypic variance, there will be one genotypic variance per treatment. In this part, we will describe briefly what is specific of such modeling with the statgenHTP package using the second example data set.

We will use the TP object phenoTParchOut in which annotated time points have been replaced by NA (see statgenHTP tutorial: 2. Outlier detection for single observations).

We can first check the number of time points containing data for a given trait:

countValid(phenoTParchOut, "LeafArea")
#> 2017-04-13 2017-04-14 2017-04-15 2017-04-16 2017-04-17 2017-04-18 2017-04-19 
#>        815       1346       1666       1665       1669       1671       1192 
#> 2017-04-20 2017-04-21 2017-04-22 2017-04-23 2017-04-24 2017-04-25 2017-04-26 
#>       1532        823       1673       1617       1221       1672       1072 
#> 2017-04-27 2017-04-28 2017-04-29 2017-04-30 2017-05-01 2017-05-02 2017-05-03 
#>       1673       1134       1137       1074       1134       1137       1092 
#> 2017-05-04 2017-05-05 2017-05-06 2017-05-07 2017-05-08 2017-05-09 2017-05-10 
#>       1449        782       1058       1240       1034        665        885 
#> 2017-05-11 2017-05-12 2017-05-13 2017-05-14 2017-05-15 
#>       1022       1313       1044        452        840

In this case, time point “2017-05-14” has only 455 observations, less than half of the total number of observations. It can bias the modeling at this time point and one may want to remove it before running the spatial analysis.

# getTimePoints(phenoTParchOut)
phenoTParchOut <- removeTimePoints(phenoTParchOut,
                                   timePoints = 32)

Modeling

Using the geno.decomp option when modeling will have two main consequences in the model: the geno.decomp variable(s) will be added as a fixed main effect for the grouping factor and separate variance components for the genotypes at each level of the grouping or decomposing factor (and the extraFixedFactors and/or check, if any, with SpATS only). The table below provides one example with three models:

OPTION ENGINE MODEL FITTED SPATIAL TERM
geno.decomp = “treatment” SpATS \(y\) = \(\mu\) + treatment + treatment:genotype + rowId + colId + \(\epsilon\) PSANOVA
geno.decomp = “treatment”, useCheck = TRUE, extraFixedFactors = “covar1” SpATS \(y\) = \(\mu\) + treatment + treatment:covar1 + treatment:check + treatment:genoCheck + rowId + colId + \(\epsilon\) PSANOVA
spatial = TRUE, geno.decomp = “treatment” ASReml \(y\) = \(\mu\) + treatment + treatment:genotype + rowId + colId + \(\epsilon\) AR1(rowId):AR1(colId)

NOTE: At the moment, it is not possible to use the combination of geno.decomp and what = "fixed".

Using the Phenoarch example, we will apply a genotype decomposition using the variables “Scenario” and “population”:

modPhenoSpGD <- fitModels(TP = phenoTParchOut,
                          trait = "LeafArea",
                          geno.decomp = c("Scenario", "population"),
                          timePoints = seq(from = 1, to = 33, by = 3))

Output

Extracting results and plotting from the models work exactly the same as previously. For example, the spatial plot on this data set looks like the following for one time point:

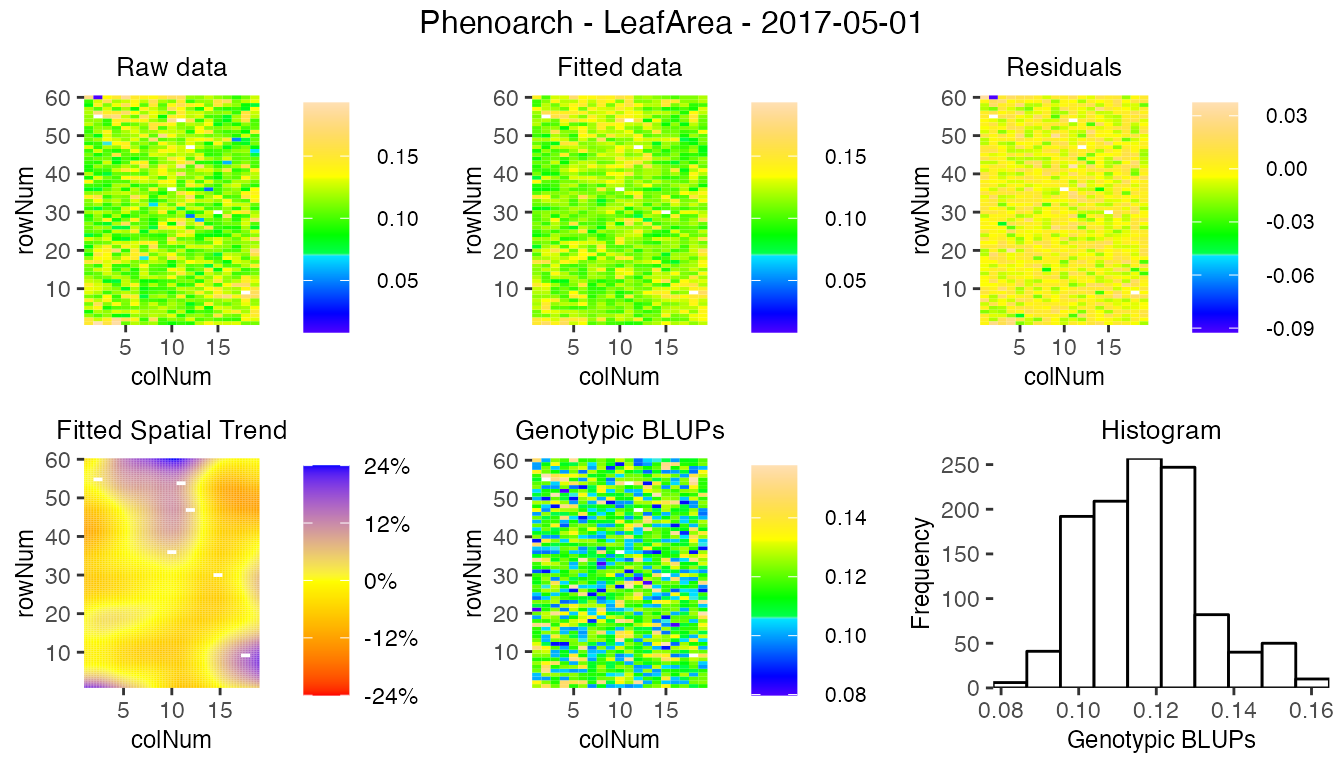
There are some significant differences in the display of some results and plots. They are highlighted below.

The predictions have two values per genotype, one for each level of the decomposition geno.decomp, here “Scenario_population”, as illustrated in the table below for three genotypes predicted from the SpATS model modPhenoSpGD.

timeNumber timePoint geno.decomp genotype predicted.values standard.errors
16 2017-04-28 WD_Panel1 GenoA01 0.0681019 0.0032738
16 2017-04-28 WD_Panel1 GenoA02 0.0812987 0.0032691
16 2017-04-28 WD_Panel2 GenoB01 0.0768258 0.0043644
16 2017-04-28 WD_Panel2 GenoB02 0.0748504 0.0043184
16 2017-04-28 WW_Panel1 GenoA01 0.0713778 0.0025793
16 2017-04-28 WW_Panel1 GenoA02 0.0802823 0.0025798
16 2017-04-28 WW_Panel2 GenoB01 0.0731051 0.0041213
16 2017-04-28 WW_Panel2 GenoB02 0.0772225 0.0041212

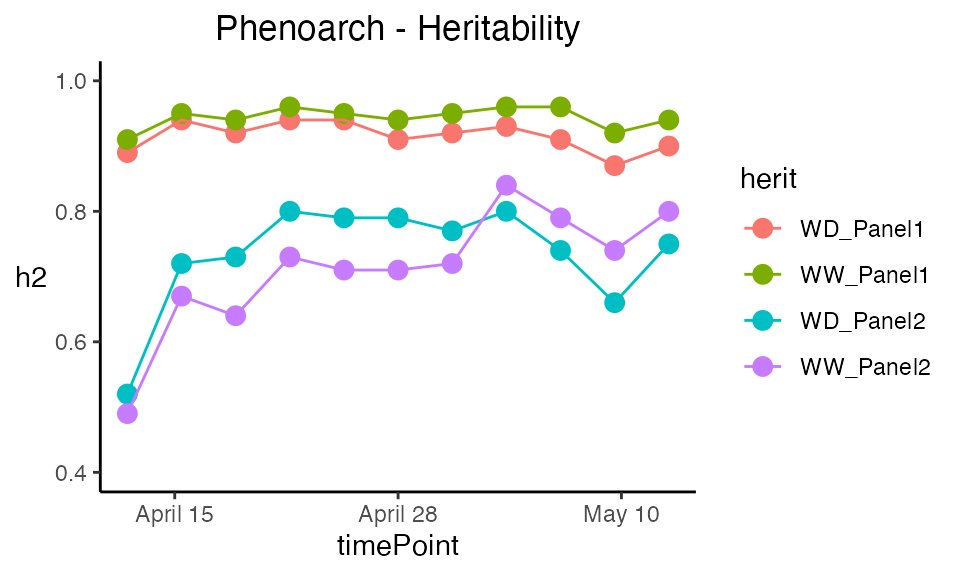
The heritabilities are now given for each of the geno.decomp levels and their plot now displays one line per level.

timeNumber timePoint WD_Panel1 WW_Panel1 WD_Panel2 WW_Panel2
1 2017-04-13 0.89 0.91 0.52 0.49
4 2017-04-16 0.94 0.95 0.72 0.67
7 2017-04-19 0.92 0.94 0.73 0.64
10 2017-04-22 0.94 0.96 0.80 0.73
13 2017-04-25 0.94 0.95 0.79 0.71
16 2017-04-28 0.91 0.94 0.79 0.71

The prediction and corrected data plots display one plot per combination genotype × geno.decomp.

References

Butler, D. G., B. R. Cullis, A. R. Gilmour, B. G. Gogel, and R. Thompson. 2017. “ASReml-R Reference Manual Version 4.” https://www.vsni.co.uk/.

Cabrera-Bosquet, Llorenç, Christian Fournier, Nicolas Brichet, Claude Welcker, Benoît Suard, and François Tardieu. 2016. “High-Throughput Estimation of Incident Light, Light Interception and Radiation-Use Efficiency of Thousands of Plants in a Phenotyping Platform.” New Phytologist 212 (1): 269–81. https://doi.org/10.1111/nph.14027.

Cullis, B. R., A. B. Smith, and N. E. Coombes. 2006. “On the Design of Early Generation Variety Trials with Correlated Data.” Journal of Agricultural, Biological, and Environmental Statistics 11 (4): 381–93. https://doi.org/10.1198/108571106X154443.

Lee, Dae-Jin, María Durbán, and Paul Eilers. 2013. “Efficient Two-Dimensional Smoothing with P-Spline Anova Mixed Models and Nested Bases.” Computational Statistics & Data Analysis 61 (May): 22–37. https://doi.org/10.1016/j.csda.2012.11.013.

Pérez-Valencia, Diana M, María Xosé Rodríguez-Álvarez, Martin P Boer, Lukas Kronenberg, Andreas Hund, Llorenç Cabrera-Bosquet, Emilie J Millet, and Fred A van Eeuwijk. 2022. “A Two-Stage Approach for the Spatio-Temporal Analysis of High-Throughput Phenotyping Data.” Scientific Reports 12 (1): 1–16. https://doi.org/10.1038/s41598-022-06935-9.

Rodríguez-Álvarez, María, Martin P. Boer, Fred van Eeuwijk, and Paul H. C. Eilers. 2018. “Correcting for Spatial Heterogeneity in Plant Breeding Experiments with P-Splines.” Spatial Statistics 23 (October): 52–71. https://doi.org/10.1016/j.spasta.2017.10.003.

Velazco, Julio G., María Xosé Rodríguez-Álvarez, Martin P. Boer, David R. Jordan, Paul H. C. Eilers, Marcos Malosetti, and Fred A. van Eeuwijk. 2017. “Modelling Spatial Trends in Sorghum Breeding Field Trials Using a Two-Dimensional P-Spline Mixed Model.” Theoretical and Applied Genetics 130 (7): 1375–92. https://doi.org/10.1007/s00122-017-2894-4.

Welham, Sue, Brian Cullis, Beverley Gogel, Arthur Gilmour, and Robin Thompson. 2004. “Prediction in Linear Mixed Models.” Australian & New Zealand Journal of Statistics 46 (3): 325–47. https://doi.org/10.1111/j.1467-842X.2004.00334.x.