Skip to contents

statgenHTP tutorial: 6. Estimation of parameters from time courses

Emilie Millet, Bart-Jan van Rossum, Martin Boer, Fred van Eeuwijk, Diana M. Pérez-Valencia, María Xosé Rodríguez-Álvarez

2022-12-13

Source: vignettes/vignettesSite/ParameterEstimation_HTP.Rmd
ParameterEstimation_HTP.Rmd

Introduction

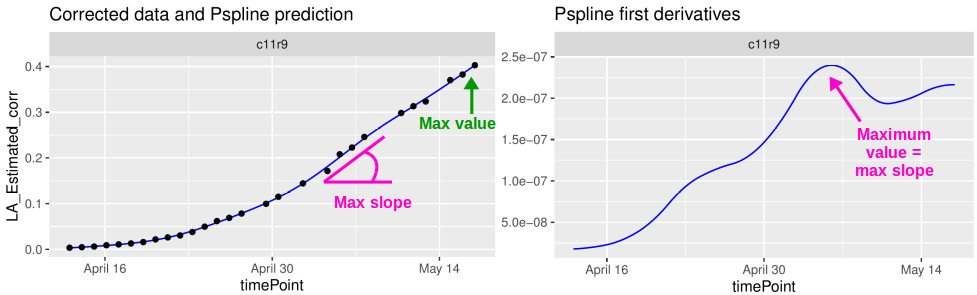
This document presents the final step of the HTP data analysis: extracting interesting parameters from the modeled time courses (Brien et al. 2020). For example, in the second data set from the PhenoArch platform, the maximum leaf area (from the P-splines) or the maximum leaf growth rate (from the first derivatives) are relevant parameters (see figure below). We could assess their variability in the genotypes and the difference between treatments, e.g. has the water scenario decreased the maximum leaf area?

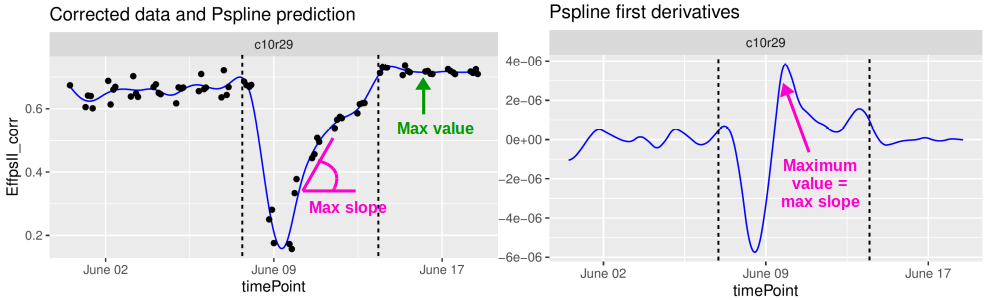
It is also possible to specify a period for the parameter estimation. For example, in the first data set from the Phenovator platform, we can select the period with the high light intensity (see figure below) and estimate the maximum slope during that period (from the first derivatives). This could be interpreted as a recovery rate of the photosystem II efficiency.

These parameters could then be further analyzed, for example in a GxE analysis (see statgenGxE), or a genetic analysis (see statgenGWAS).

The functions described in this tutorial can be applied to corrected data, genotypic means (BLUEs or BLUPS) (see statgenHTP tutorial: 3. Correction for spatial trends), curves obtained from the P-splines hierarchical data model (see statgenHTP tutorial: 5. Modelling the temporal evolution of the genetic signal), or on raw data. It allows estimating maximum, minimum, mean, area under the curve (auc) or percentile using predicted values, first or second derivative, during a given period or for the whole time course.

Estimation of parameters from curves

Example 1

We will use the fit.splineNumOut previously created (see statgenHTP tutorial: 4. Outlier detection for series of observations). It contains the P-spline prediction on a subset of plants without the time course outliers. We will estimate the area under the curve of the trait:

subGenoVator <- c("G070", "G160", "G151", "G179", "G175", "G004", "G055")
paramVator1 <- 
  estimateSplineParameters(x = fit.splineNumOut,
                           estimate = "predictions",
                           what = "AUC",
                           timeMin = 330,
                           timeMax = 432,
                           genotypes = subGenoVator)

plot(paramVator1, plotType = "box")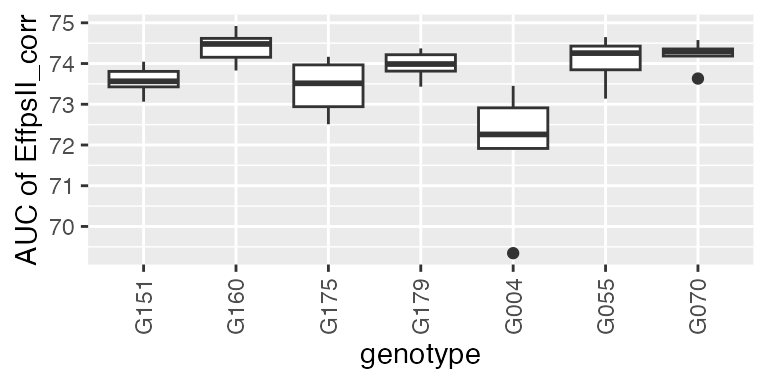

For this subset of genotypes, there is a variability in AUC of the psII efficiency. This could be used in genetic analysis and maybe to perform a GWAS.

Another example is using the derivative during the recovery period (at the end of the time course, so after the light change) to get the maximum slope, or the maximum rate of the psII per time unit during this period.

paramVator2 <-
  estimateSplineParameters(x = fit.splineNumOut,
                           estimate = "derivatives",
                           what = "max",
                           timeMin = 210,
                           timeMax = 312,
                           genotypes = subGenoVator)

plot(paramVator2, plotType = "box")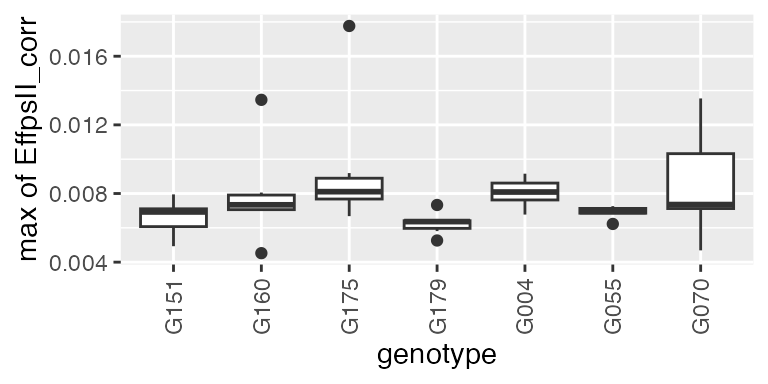

Note: when “min” or “max” is selected, the output also contains the parameter occurence time point, as numerical timeNumber and date timePoint. See in the table below:

genotype plotId max_derivatives max_timeNumber max_timePoint
G004 c11r55 0.0067723 227.7778 2018-06-10 04:23:40
G004 c13r20 0.0084969 226.0000 2018-06-10 02:37:00
G004 c19r15 0.0073183 232.0000 2018-06-10 08:37:00
G004 c21r45 0.0091547 223.3333 2018-06-09 23:57:00
G004 c24r48 0.0080870 224.2222 2018-06-10 00:50:20
G004 c2r15 0.0079295 226.0000 2018-06-10 02:37:00

Example 2

For this example, we will use the genotypic prediction (BLUPs, see statgenHTP tutorial: 3. Correction for spatial trends) available in the spatPredArch data set. We will fit P-splines at the genotypic level using the geno.decomp levels defined in the spatial model.

data(spatPredArch)  
fit.splineGenoArch <- fitSpline(inDat = spatPredArch, 
                                trait = "predicted.values",
                                knots = 15,
                                minNoTP = 18)

plot(fit.splineGenoArch, 
     genotypes = "GenoA36")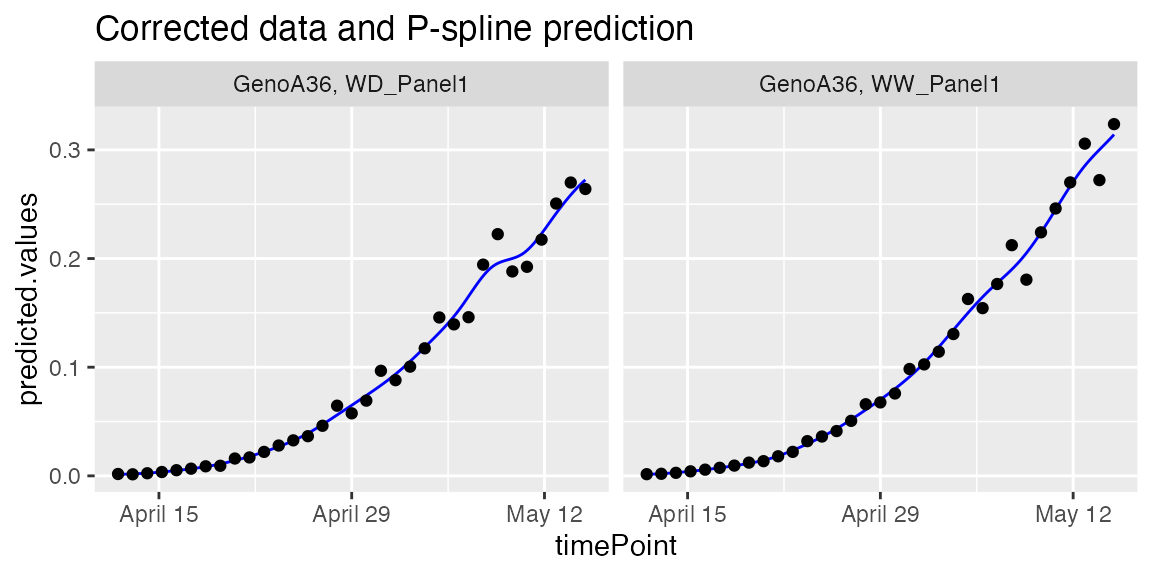

We can estimate the maximum value of the leaf area from the predicted P-splines:

paramArch1 <-
  estimateSplineParameters(x = fit.splineGenoArch,
                           estimate = "predictions",
                           what = "max")
plot(paramArch1, plotType = "hist")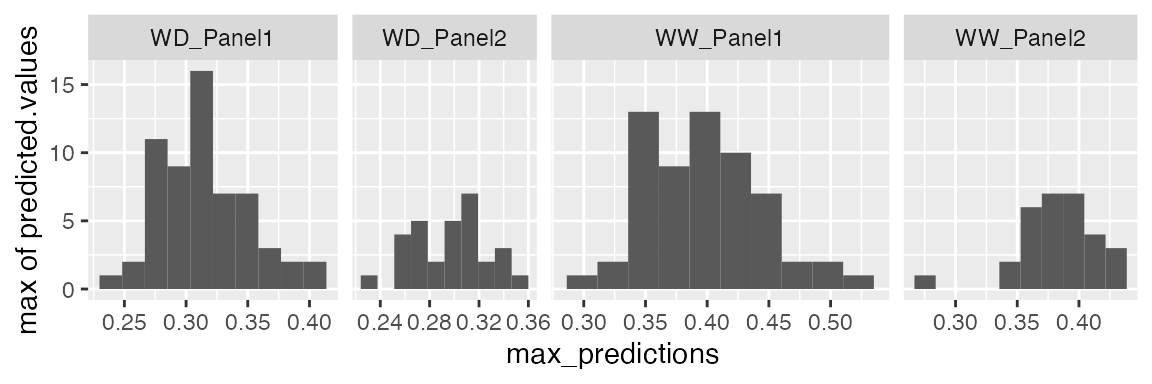

Example 3

For this example, we will use curves obtained from the P-splines hierarchical data model (see statgenHTP tutorial: 5. Modelling the temporal evolution of the genetic signal). We can use psHDM objects (that is, objects obtained from fitSplineHDM() (fitted curves) or predict.psHDM() (predicted curves)). For this example, we will use predicted curves.

## The data from the Phenovator platform have been corrected for spatial
## trends and outliers for single observations have been removed.

## We need to specify the genotype-by-treatment interaction.
## Treatment: water regime (WW, WD).
spatCorrectedArch[["treat"]] <- substr(spatCorrectedArch[["geno.decomp"]],
                                      start = 1, stop = 2)
spatCorrectedArch[["genoTreat"]] <-
  interaction(spatCorrectedArch[["genotype"]],
             spatCorrectedArch[["treat"]], sep = "_")

## Fit P-Splines Hierarchical Curve Data Model for all genotypes.
fit.psHDM  <- fitSplineHDM(inDat = spatCorrectedArch,
                           trait = "LeafArea_corr",
                           pop = "geno.decomp",
                           genotype = "genoTreat",
                           plotId = "plotId",
                           difVar = list(geno = FALSE, plot = FALSE),
                           smoothPop = list(nseg = 5, bdeg = 3, pord = 2),
                           smoothGeno = list(nseg = 5, bdeg = 3, pord = 2),
                           smoothPlot = list(nseg = 5, bdeg = 3, pord = 2),
                           weights = "wt",
                           trace = FALSE,
                           useTimeNumber = FALSE)

## Predict the P-Splines Hierarchical Curve Data Model on a dense grid
## Only predictions (and standard errors) are obtained  
## at the population and genotype levels
pred.psHDM <- predict(object = fit.psHDM,
                      newtimes = seq(min(fit.psHDM$time[["timeNumber"]]),
                                     max(fit.psHDM$time[["timeNumber"]]),
                                     length.out = 100),
                      pred = list(pop = TRUE, geno = TRUE, plot = TRUE),
                      se = list(pop = TRUE, geno = TRUE, plot = FALSE),
                      trace = FALSE)

Although we have available information at population, genotype and plot levels, this function only extracts information at genotype and plot levels. Nevertheless, we are generally interested in the genotype level. For example, in the paper by Pérez-Valencia et al. (2022), they extracted three features:

  • The maximum spatially corrected leaf area (from estimated genotype-specific trajectories)
##  From estimated genotype-specific trajectories
plot(pred.psHDM, plotType = "popGenoTra", themeSizeHDM = 4)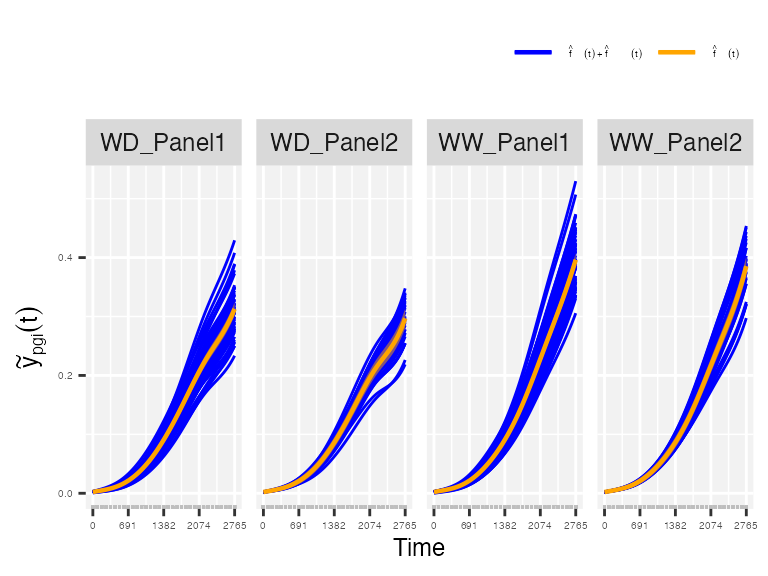

## Estimate maximum spatially corrected leaf area.
paramArch1 <- estimateSplineParameters(x = pred.psHDM,
                                     what = "max",
                                     fitLevel = "geno",
                                     estimate = "predictions")

## Create a boxplot of the estimates.
plot(paramArch1, plotType = "box")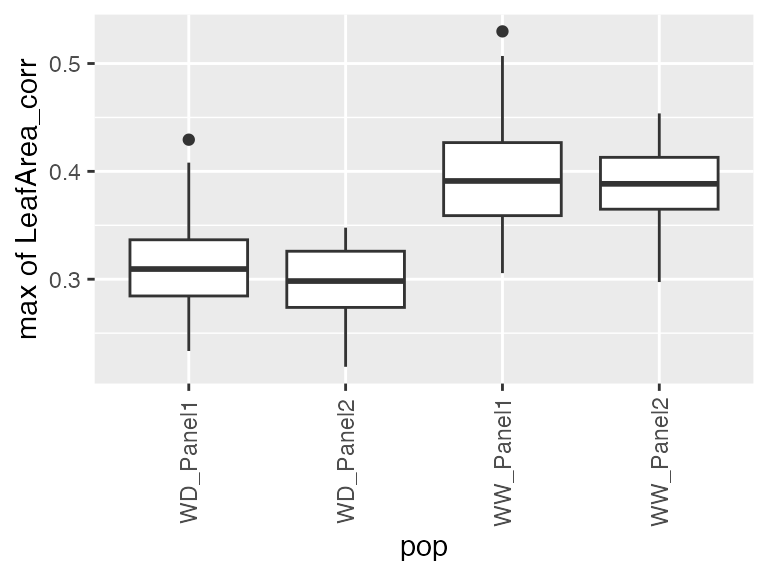

  • The maximum speed rate (from the first derivative of the estimated genotype-specific trajectories)
## From the first derivative of the estimated genotype-specific trajectories
plot(pred.psHDM, plotType = "popGenoDeriv", themeSizeHDM = 4)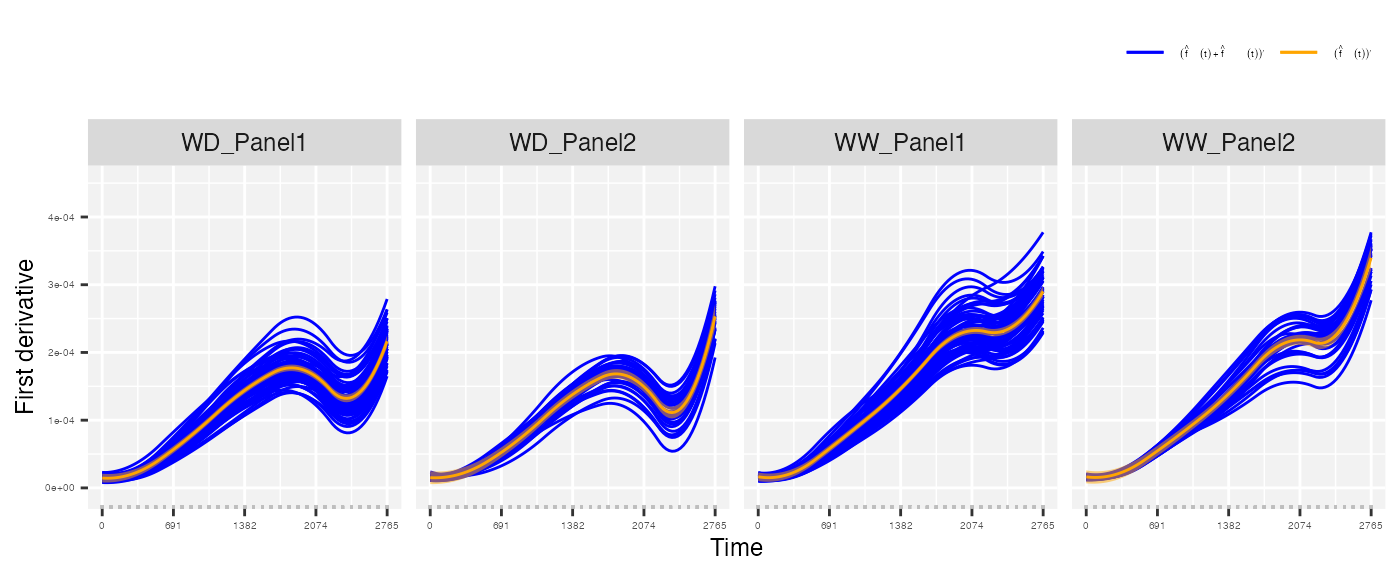

## Estimate maximum speed rate 
## We are interested on a local maximum (before timeNumber 2500)
paramArch2 <- estimateSplineParameters(x = pred.psHDM,
                                     what = "max",
                                     fitLevel = "geno",
                                     estimate = "derivatives",
                                     timeMax = 2500)

## Create a boxplot of the estimates.
plot(paramArch2, plotType = "box")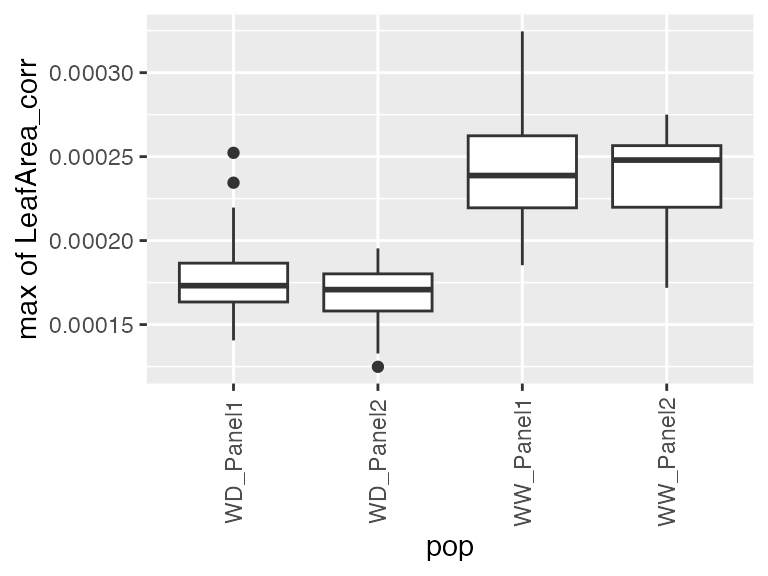

  • The area under the estimated genotype-specific deviations, as follows
## From the estimated genotype-specific deviations
plot(pred.psHDM, plotType = "genoDev", themeSizeHDM = 4)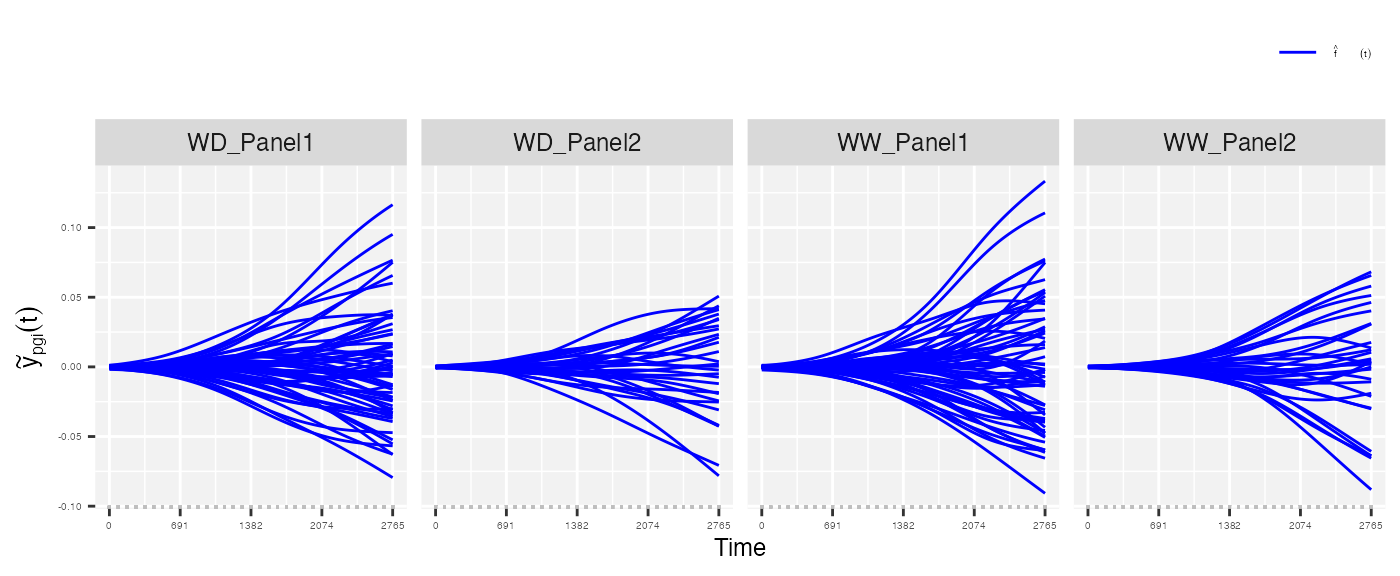

## Estimate area under the curve (AUC).
paramArch3 <- estimateSplineParameters(x = pred.psHDM,
                                     what = "AUC",
                                     fitLevel = "genoDev",
                                     estimate = "predictions")

## Create a boxplot of the estimates.
plot(paramArch3, plotType = "box")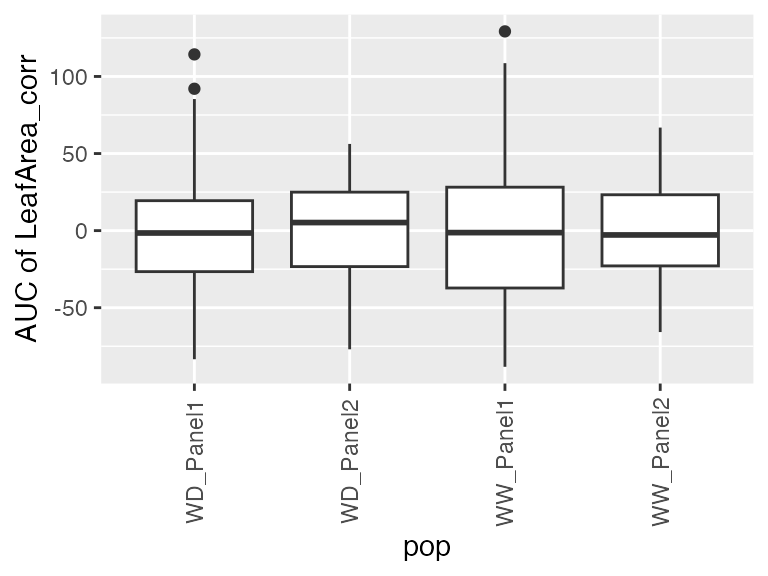

Example 4

For this example, we will use the raw data from the RootPhAir, corrected for individually outlying observations (see statgenHTP tutorial: 2. Outlier detection for single observations) and time course outliers (see statgenHTP tutorial: 4. Outlier detection Time course). We will fit P-splines at the plant level on a subset of genotypes.

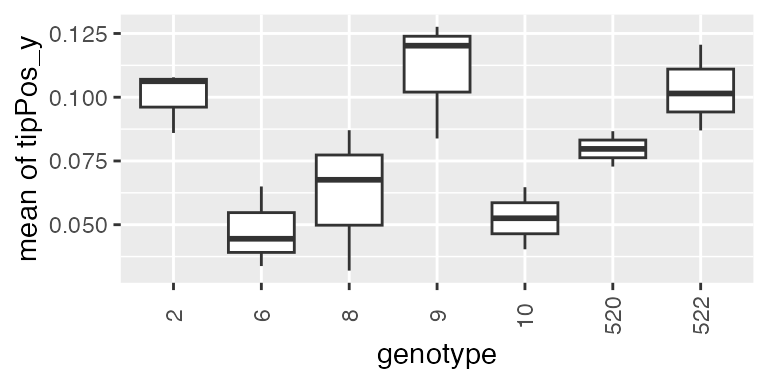
subGenoRoot <- c( "2","6","8","9","10","520","522")
fit.splineRootOut <- fitSpline(inDat = noCorrectedRootOut,
                               trait = "tipPos_y",
                               knots = 10,
                               genotypes = subGenoRoot,
                               minNoTP = 0,
                               useTimeNumber = TRUE,
                               timeNumber = "thermalTime")

We will then estimate the mean growth rate using what = "mean" for the subset of genotypes:

paramRoot1 <-
  estimateSplineParameters(x = fit.splineRootOut,
                           estimate = "derivatives",
                           what = "mean")

plot(paramRoot1, plotType = "box")

References

Brien, Chris, Nathaniel Jewell, Stephanie J. Watts-Williams, Trevor Garnett, and Bettina Berger. 2020. “Smoothing and Extraction of Traits in the Growth Analysis of Noninvasive Phenotypic Data.” Plant Methods 16 (1): 36. https://doi.org/10.1186/s13007-020-00577-6.

Pérez-Valencia, Diana M, María Xosé Rodríguez-Álvarez, Martin P Boer, Lukas Kronenberg, Andreas Hund, Llorenç Cabrera-Bosquet, Emilie J Millet, and Fred A van Eeuwijk. 2022. “A Two-Stage Approach for the Spatio-Temporal Analysis of High-Throughput Phenotyping Data.” Scientific Reports 12 (1): 1–16. https://doi.org/10.1038/s41598-022-06935-9.